ダイエットの経済的価値を試算してみた

SNSでシェア
目次
先日、とある研究結果を見つけました。
愛知の健康保険協会による
というレポートです。
このレポートでは標準的なBMI値から逸脱するほど、年間平均医療費が増えるという結果になっていました。肥満になるほど不健康で病気になる確率は高いイメージではあるので、直感的にも理解しやすい結果です。
このレポートを見た時にふと、「BMI値と医療費を法則化できるなら、将来かかる医療費への影響値としてダイエットの効果を計算できるのでは?」という考え、ザックリ試算してみました。
①分析課題
将来かかる医療費への影響値としてダイエットの経済的効果を法則化すること
②前提
・BMIと医療費の関係性は前述の※1を参考に用いるとする。
(しかし、元データ及びモデル式は不明なため、レポート内グラフの縦軸・横軸値の値を参考にそれっぽいモデルを作成。今回試算に使った式は以下の通り。また参考では男性・女性間でもモデルが若干異なるものの、目分量になるので区別はせずに考えております。)
年間医療費 = 631.313×BMI^2 – 24,873.737×BMI+ 331,439.394
・レポートには明確な記載はなかったが、研究当時の同年代国民1人あたり医療費の額と比較すると約3割程度だったため、自費負担額で計算されていると想定。
・医療費相場については、分析時最新の2019年データに基づいて計算するものとする。(将来的の医療費相場の変動は加味しない)
・モデルのサンプル条件が35 歳~74 歳であったため、試算対象とする医療費は「35歳~74歳までの医療費」とし、35歳~74歳までの医療費を生涯医療費とする。
プロセス1.直近の医療費相場の反映
データが平成20年の研究データで10年以上前のデータであったため、現在とは相場が大きく異なっていると考えられる。そこで、政府の統計情報サイト(e-start)で現在と当時でどの程度医療費相場が変化しているかを検証。
直近のデータは2019年の国民医療費(第8表 国民医療費・構成割合・人口一人当たり国民医療費,診療種類・性・年齢階級別)より、当時のデータとしては2008年の国民医療費(第12表 性、年齢階級、診療種類別国民医療費及び人口一人当たり国民医療費)を使用※2
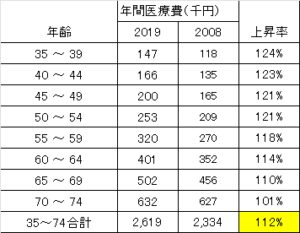
人口一 人当たり国民医療費(千円)の35歳~74歳までの医療費を比較
これより医療費は35歳~74歳までにかかる医療費は112%上昇しているといえる。
そのため、本分析では以下の式を35歳~74歳までの医療費を生涯医療費として用いるとする。
生涯医療費 = (631.313×BMI^2 – 24,873.737×BMI+ 331,439.394)× 112% × 40 (※3)
プロセス2. 消費カロリーをBMI値に換算
次に運動して消費したカロリーとBMI値の法則化を行う。
カロリーに関してはタニタの「カロリーとは」より、以下の記述を参考にしました。
”体内に貯蔵されている脂肪1kg(1,000g)を消費するにはどれだけのカロリーが必要になるのでしょうか?
脂肪1gは9kcalなので、1kgの脂肪を消費するには9000kcalのカロリーが必要かといえばそうではありません。人間の脂肪は「脂肪細胞」として蓄えられているので、全てが純粋な脂肪というわけではありません。脂肪細胞の約8割は脂質(あぶらの塊)ですが、残り2割ほどは水分や細胞を形成するさまざまな物質で構成されています。
これを踏まえて計算すると脂肪1kgを消費するのに必要なエネルギー(カロリー)は、9kcal×1000g×80%=約7200kcal 程になります。”
もちろん、ダイエットで消費したカロリーが全て脂肪を消費するとは限りませんが、一旦全て脂肪で消費したと仮定すると、7200kcal消費すると1kgのダイエット効果となります。(実は筆者は昔レコーディングダイエットをしたことがあったのですが、その際に消費カロリーと体重変化をこの水準で計算すると概ね一致していたので結構信頼しています)
またBMI値は以下の通りです。
BMI = 体重(kg) ÷ 身長(m)^2
つまり先ほどのカロリー計算に直すと
BMIの変化 = カロリー変化(kcal) / [7200 × 身長(m)^2 ] (※4)
となりますね。
プロセス3. 消費カロリーから経済的価値を計算
よって※3と※4の式を計算することでカロリーの生涯医療費への影響値をとして経済的価値を計算できます。
身長ごとに適切なBMI値が異なるため、一律に何kgの人が何kcal消費するといくら、という形にはなりませんので参考までに、身長165cmの人、170cmの人、175cmの人のパターンで以下に試算しています。
身長175cmの人の場合

身長170cmの人の場合

身長165cmの人の場合

以上の様になります。この表を見れば、自分の現在の身長と体重から、ザックリ100kcal消費した運動をしたときの生涯医療費の変化が分かりますね。
例えば身長170cm、体重75kgの人が、100kcal消費する運動を能動的に行った場合は、生涯の医療費を約1600円節約したことになります。
逆に、食べなくてもいいのにとりあえず食べる様な無駄な接種をしてしまった場合、つまり100kcalを無駄にとってしまった場合は生涯の医療費を約1600円増やす事になります。
20円で60kcalくらいの一口サイズのチョコレートなら、もしそれを食べなかったとしても全く同じ生活をしていた場合、実は約1000円分損をしているのかもしれません。
運動で100kcal消費しても、理論上は0,1kgも脂肪は落とせません。ですが将来の医療費を1600円減らせるならちょっとやる気になりませんか?
一方で痩せすぎもよくないことが分かります。標準的なBMIよりも体重が少なすぎても、不健康で医療費は平均的には増えるのです。
あとがき
もちろん、理想的なBMI値=健康とは限りません。ダイエットも痩せ方次第では逆に不健康になってしまう事もあるでしょう。あくまで、そのBMI値の平均的な人のデータであって、個別には様々な事情があります。
ですのでBMIだけを判断基準に考えるのもあまりよくありませんが、こういった観点から一度自らの食生活や生活習慣を見直してみてはいかがでしょうか?
ここでは35歳~74歳のうちにかかる医療費を生涯医療費としています。75歳以降や35歳未満だとBMIよりもその他の病気の原因の方が多そうなので、生活習慣要因での差分を考えるならザックリこの数字でもいいのではないかなとは考えています。
*参考:35歳以上で現在の年齢に合わせて推計したい場合
ここでは35歳~74歳時の合計を将来の生涯医療費としていますが、既に40代、50代の方もいらっしゃるとおもいます。しかし、医療費は年齢が増える程高くなる傾向にあるので、ザックリ年数で割っても精緻なモノは計算できません。
上述の表に対して、ご自身の年齢に合わせて、下表の黄色の比率をかけていただいたものが、ザックリ、将来の医療費への影響値になりますのでよろしければご参考ください。