デュレーションってなに?デュレーションの意味と計算式【投資用語解説】

SNSでシェア
目次
デュレーションとは?
『デュレーション』という言葉をご存知でしょうか?
主に債券投資で使われる指標で英語表記では『Duration』と綴ります。
デュレーションとは、ザックリ言うと「投資の平均回収期間を示す指標」です。
この指標が小さい程回収期間が短く、大きいほど回収期間が長いと考えて構いません。そしてこの指標は小さければ小さいほど良いです。
なぜデュレーションは重要なのか?
投資において、回収期間は非常に重要な指標です。回収期間が短ければ短いほど、投資のデフォルトリスク(例えば投資先の会社が倒産して債券が回収できなくなるリスク)は小さくなります。
早期に回収できれば再投資をすることも可能で、結果的に大きな収益も得られます。
ではそれなら「投資が完了するまでの長さ」で見れば良いのでは?となると思います。
しかし投資はそれほど単純ではありません。回収するタイミングと金額の大きさも非常に重要なのです。
そして、それらを考慮して『投資の回収期間』を評価できるのがこのデュレーションなのです。
ちょっとややこしいですが具体的な例を挙げて説明します。
例えば、残存期間5年の債券に投資する2つの場合を考えましょう。
- 価格100万円で購入し、5年後に120万円が返ってくる
- 価格100万円で購入し、1年後に100万円・2~5年後に毎年5万円が返ってくる。
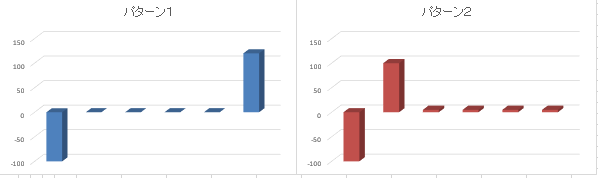
上記の2つの投資はどちらも投資の回収期間は5年で、回収金額も100万の投資に対して120万で同じです。
しかし、それぞれ回収するタイミングが異なります。ではどちらの方が好ましい投資でしょうか?
間違いなく2のパターンですよね。
2の場合なら2年目以降に債券がデフォルト(回収不能になっても)しても初期の投資額を回収できるからです。
また1年目後に100万円を回収できれば、その100万円を使って同じ債券に再投資をすることも可能です。
この両者のデュレーションを計算すると以下の様になります。
パターン1・・・ 5.0
パターン2・・・ 1.3
すると投資の完了するまでの期間だけでみるとどちらも5年で同じですが、デュレーションではパターン2<パターン1となり、パターン2の方が小さくなります。
つまり、デュレーションで比較することで、早いタイミングで出来るだけ多くの額が回収出来るという事も考慮して比較をすることが可能になります。
すなわち、デュレーションとは投資リスクや収益性を測る一種の指標と見ることが出来ます。
マコーレ・デュレーション
一般的にデュレーションと言われるものがマコーレ・デュレーションです。
計算式ではマコーレ・デュレーション = 投資に対する平均回収期間 と表されます。
*若干数学的な話に入るので数字が苦手な方は、この節は読み飛ばして頂いて構いません。
計算式:
*Dmac:マコーレ・デュレーション
CFt: t期キャッシュフロー・・・t期(t年後)にいくらお金がもらえるのか?
r : 割引率 ・・・この投資(債券)の利率(年間の金利)
ここでCFtを1+rのt乗で割ったものは、t期キャッシュフローの現在価値となっています。
つまり、マコーレ・デュレーションとはキャッシュフローの現在価値で期間を加重平均したものとなっているのです。
※現在価値に落とし込んだ時に、回収額が大きいキャッシュフローの年により重みづけがされるような計算となるということです。
先ほどの例で説明すると、パターン1であれば1年後にキャッシュフロー集中しているのでより1に重みづけを、パターン2であれば5年後にキャッシュフローが集中しているので5に重みづけをした平均となります。
ちなみに債券の価格は、その債権から得られるキャッシュフローの現在価値の合計と等しくなっています。つまり、先述の式の÷記号の右側の項はそのまま債券価格となっています。
*P:債券価格
*CFt: t期キャッシュフロー・・・t期(t年後)にいくらお金がもらえるのか?
r : 割引率 ・・・この投資(債券)の利率(年間の金利)
修正デュレーション
またデュレーションの指標としてはもう一つあります。それが修正デュレーションです。修正デュレーションは計算上では上記のマコーレ・デュレーションを1回割り引いたものとして表されます。
計算式:

*CFt: t期キャッシュフロー・・・t期(t年後)にいくらお金がもらえるのか?
r : 割引率 ・・・この投資の利率(年間の金利)
なので修正デュレーションも基本的には投資の回収期間を示すものと考えて構いません。
しかし、修正デュレーションにはもう一つ重要な意味があります。
それは利回り変化に対する投資価値(債券価格)の変動率です。
債券は利回りが変わるとその価値も変わります。たとえば修正デュレーションが1の債券投資の場合、最終利回りが2%変化すると債券価格も2%変化するという事です。同じく修正デュレーションが2の債券投資の場合は、最終利回りが2%変化すると債券価格は4%変化するということになります。
つまり修正デュレーションが大きいほど、金利変動の影響を受けやすいと取る事も出来ます。
*ここから先も若干数学的な話に入るので数字が苦手な方は、この節は読み飛ばして頂いて構いません。
なぜ?この修正デュレーションが利回り変化に対する債券価格の変動率になるのか?というと以下の様な関係式となっているからです。
債券価格Pとすると
債券価格Pの金利rに対する変動率は、Pをrで微分したものなので、修正デュレーションDと以下のような関係となります。
計算式:

*
P: 投資価値
r: 利回り(=投資家の期待する割引率)
Dmac: マコーレ・デュレーション
P: 債券価格
D: 修正デュレーション
つまり「債券価格Pの金利rに対する変動=ー修正デュレーション×債券価格P」という関係性になっているのです。
また符号はマイナスなので修正デュレーションが1ということは、金利が2%上がると債券価格は2%下がるという事になります。
まとめ
デュレーションに関して記載してきましたが、いかがだったでしょうか?
マコーレとか修正とか書いてきましたけど、少し専門的なので正直普段は使わないです。笑
ですが、こんな投資の見方もあるという感じで理解頂ければ嬉しいです。
数式自体は簡単なので、Excelでベースを作ってしまえば応用が利きます。
債券を評価する一つの軸として、使用してみるのもいいかもしれないですね!
例題も用意したので、興味がある方はこちらからどうぞ。